瞎谈点积

从标题可以看出这篇文章时关于点积的。本文讨论的是平面点积。本文记 的长度为 。

参与点积运算的是两个向量。架设有两个向量 ，则我们定义点积为 。点积是一个很神奇的东西，先说它的几条性质。

性质

交换律

对于任意 ，都有 。 证明：显而易见吧。

双线性

双线性意味着一下两点：

2. 证明都不难，根据定义展开计算即可，在这里不做赘述。

正定性

其实就是非负性

正定性意味着对于任何向量 ，。取等号当且仅当 是零向量。

证明也很简单，假设 注意到 。显而易见，长度是不能为负的。

以上就是点积的三条性质，这些性质大多用来参与运算。

关系

这还不是点积最神奇的地方，最神奇的地方在于点积和两个向量的长度和夹角都有关。

1. 对于单位圆上的向量 ，其夹角为 ，都有 。

   证明：假设向量 是由 逆时针 度之后得到的，由于众所周知，逆时针旋转 度之后 的旋转矩阵是 。设 ，那么有 。所以 证毕。

2. 。

   证明：既然有了单位向量点积的关系，我们不如将这两个向量转化为单位向量。显然 都是单位向量，而且夹角的大小不变。因此 。再用双线性得，移项就可以得到 。这也说明了一点，就是两个向量垂直当且仅当点积等于一，因为这时候 。

以上两点可以看出，点积和参与运算向量的长度和夹角都有关。为什么呢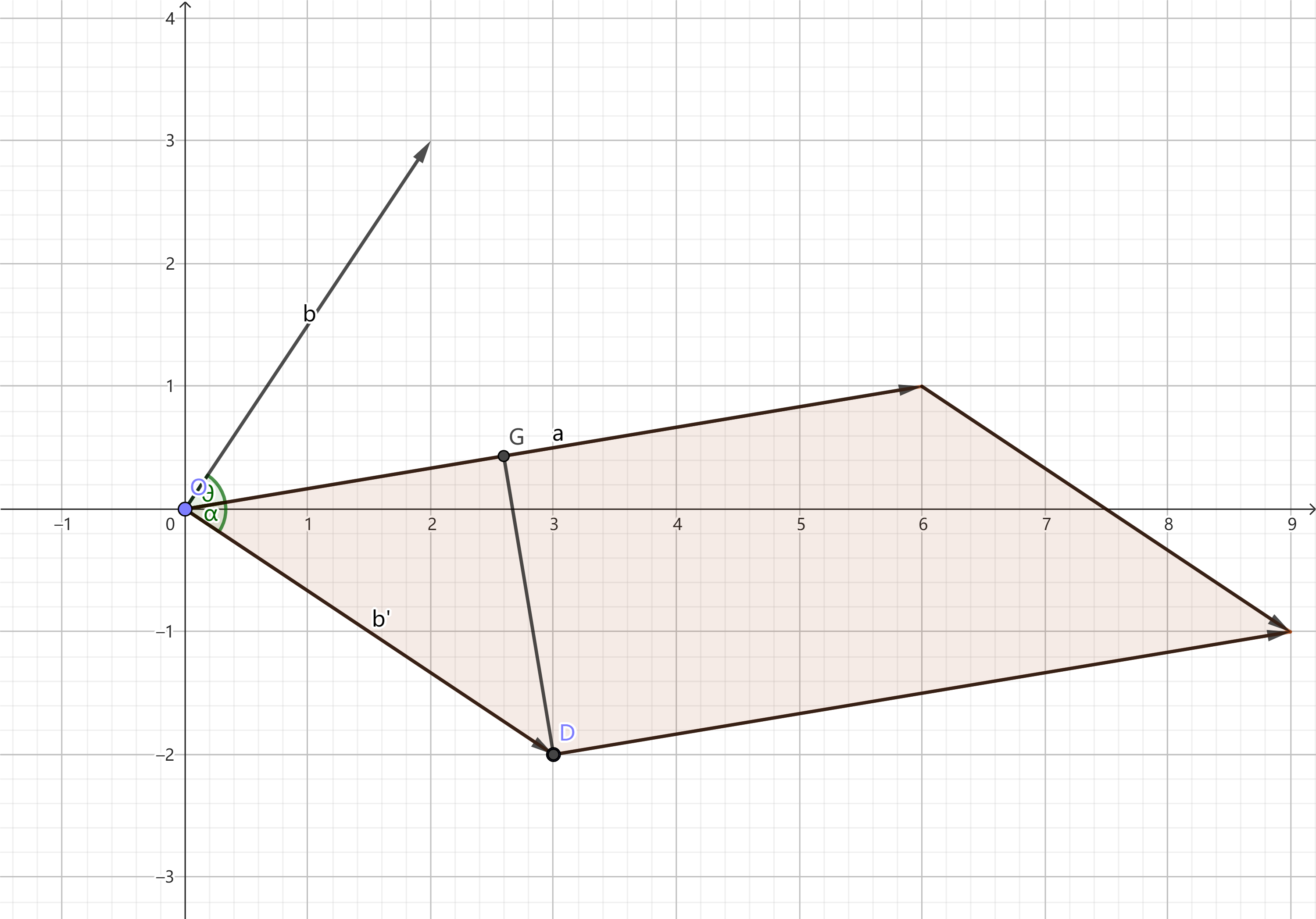？ 如图，设将 顺时针旋转 后得到 ，因此整个阴影四边形的面积就是 ，恰好是 如果你不懂行列式，也没关系。根据三角函数我们可以知道 所以平行四边形的面积为 。这样就解释了为什么点积和长度，夹角都有关系。行列式不也是吗

应用

由于这些神奇的特性，我们可以有点积做一些有趣的事情。

正交分解公式

也可以叫投影公式，起这个标题只是因为听起来更高大上。

这个公式的作用是这样的：给定两个向量 ，将 拆成 的形式，使得 。其中一个方法是线性变换，另一个就是点积。

先给出一个解析几何的方法： 假设 ，由于 ，所以我们可以设 ，可以得到 ，两边同时点积得 ，由于 ，所以 。因此 ，。带入得 。这是怎么发现的

再给出一个其他的理解方法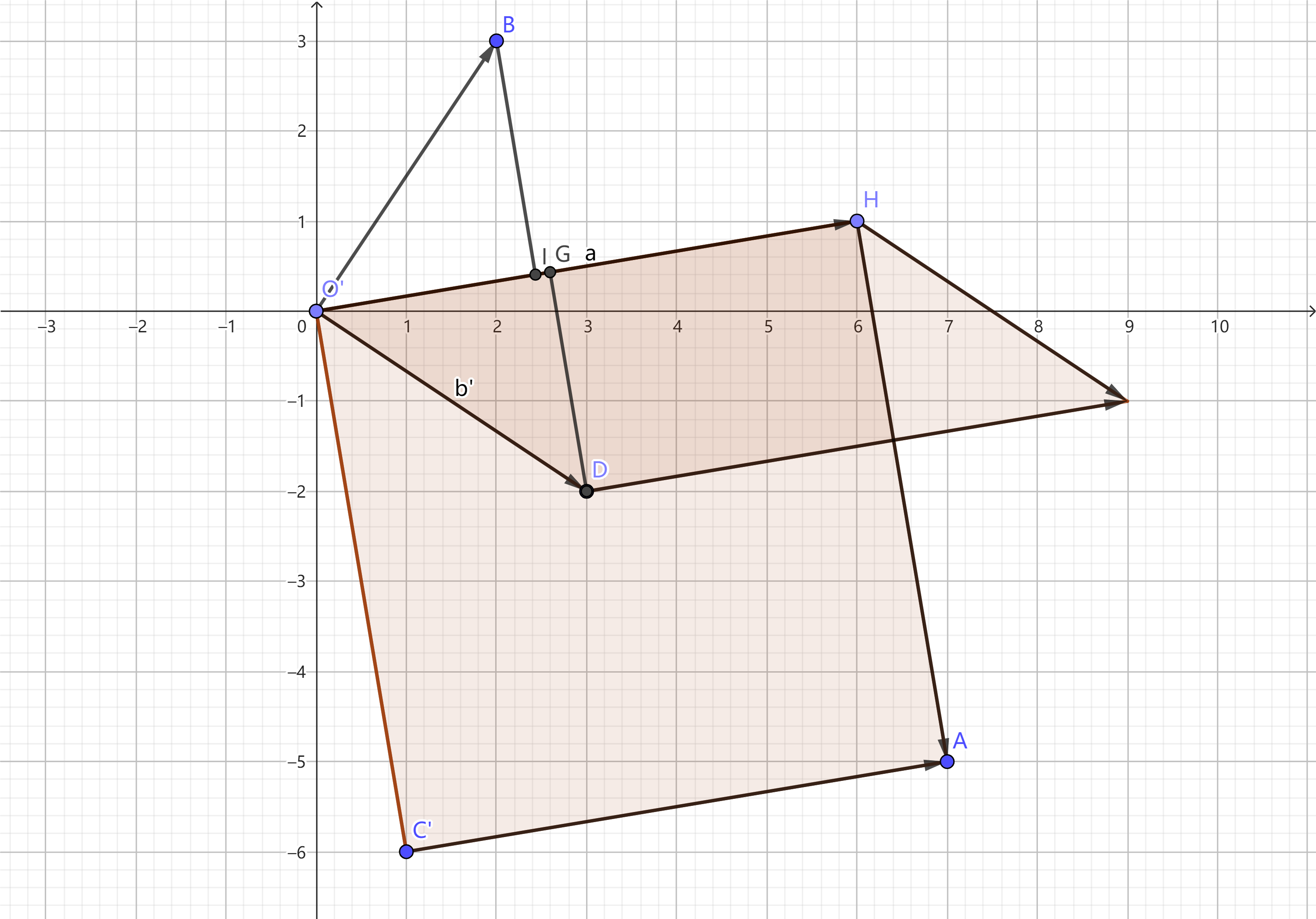： 容易看出， 实际上是 和 的比值，等于 和 的比值（通过三垂直可以知道 ）。因此将这个数乘上 自然就是 ，也就是得到的 ，太好了，数学诚不我欺。

柯西不等式

柯西不等式，又叫Cauchy-Schwarz不等式，指的是这个 。结合刚才的平行四边形和 可以很快推出来，因为 在 之间，取 时当前仅当 。

还有另外一种证明方法，就是将 进行正交分解，得 。移项得 ，两边同时点积得 整理得 证毕。