动态规划入门指北

从搜索的优化说起

考虑这样题目： >写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

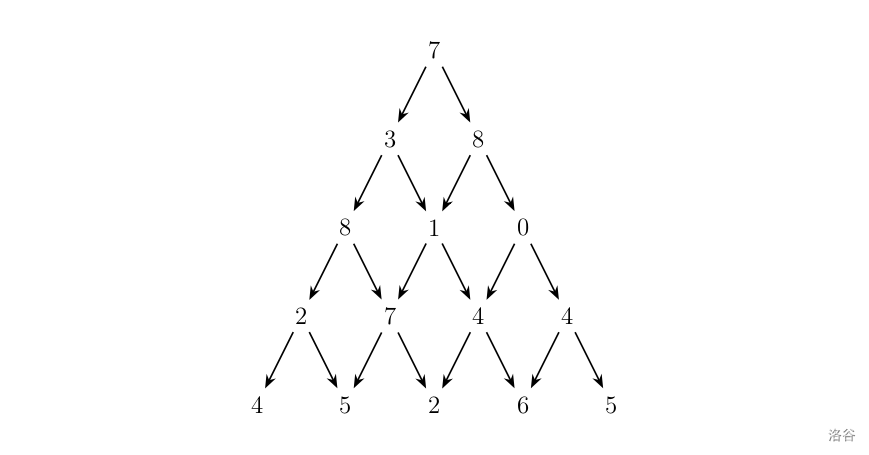
显然，我们可以从顶端开始，枚举每一条路径，求出其中的最大值。我们注意到，如果有一条路径可以到达某个点，之前的路径并不会影响之后走的路径。

举个例子：假如通过 到达了 这个点，接下来打算走 这几个点到达 这个点，但加入你通过 到达 这个点，仍然可以走 到达 。

因此，此时到达 的最优解在最后肯定比到达 的其它路径更优。因为之后无论什么路径，最有解和其他路径都可以走，而最优解有优于其他路径，因此肯定更优。比如图中 肯定比 更优，因为到达 这个点的路径更优。

所以，到达每个点的最优解只和到达上一个点的最优解有关。所以刚刚的搜索算法多了许多无效搜索。因为每个点的前面一个点只有两种可能（左和右两个点，最优解记作 和）因此，如果将当前的数字记作 ，到达下一个点的最优路径为 。我们只要枚举每层每个点，像这样求出最优解即可。像这样的算法叫做动态规划（Dynamic Programming，简称DP）。

动态规划简介

接下来更加详细的介绍动态规划算法。

概念解释

1. 在上面的例子中，求出 要先求出 和 。我们将求出 称为 的”子问题“，通常，子问题是一个数据规模更小的相同问题。
   
2. 在上文中，我们用点上的数字来描述一个问题，比如“到编号为 的点的最有解”，但实际上可能会优重复，而且查找并不方便。因此我们可以用行号列号来描述一个问题。比如“到第 行第 个点的最优解”。像这样描述一个子问题，叫做“状态”。
   
3. 在上面的例子中，我们按照行号枚举每个点。在这里，我们将一行的点分为一类，从上到下枚举。其中一类被称为动态规划的阶段，设计阶段时要保证，在解决一个问题前，要保证问题的所有子问题都被正确解决。
   
4. 上文的 描述了如何从一个状态的到下一个状态（从子问题的最优解推导出问题的最优解），被称为“状态转移方程”。

接下来考虑动态规划要满足的条件：

最优子结构

所谓最优子结构，是指以下两点

1. 到达每个状态前做出的决策并不会影响之后做出的决策（对应上文如果有一条路径可以到达某个点，之前的路径并不会影响之后走的路径）
   
2. 问题的最优解一定来自于子问题的最优解（对应上文到达每个点的最优解只和到达上一个点的最优解有关）

无后效性

无后效性是指，一个子问题的答案只依赖于在它之前解决子问题，不会受在它之后解决的子问题的影响。

在开头的例子中，经过了一个点是不能往回走到，因此满足无后效性。

重叠子问题

重叠子问题是指，要解决多个问题往往依赖于一些相同的子问题。比如开头的例子中，求第 行第 和第 个数都依赖于第 行第 个数的最优解。重叠子问题越多，dp算法效率越高。

和其他算法的关系

分治

DP可以看作是一种分治算法，将一个问题分解成多个子问题，当子问题足够容易解决时解决掉这些子问题，再用状态转移方程得到问题答案。  分治算法通常用递归来实现，我们也可以写出DP的递归写法（以开头的数字三角形为例）：

int slove(int i,int j){
    if(dp[i][j]!=0)return dp[i][j];
    if(i==1)return dp[i][j]=arr[i][j];
    else return dp[i][j]=max(slove(i-1,j-1),slove(i-1,j))+arr[i][j];
}

递归的运算次数再某些情况下会略小于接下来要说的递推写法，但是由于函数调用需要花时间，并且递归层数过深容易爆栈，因此采用递归写法实际上不一定比递推更优。

递推

实际上，按阶段枚举每个点和递推也很是相似，都是通过子问题的解推出问题的解。

dp[1][1]=arr[1][1];
for(int i=1;i<=r;i++){
    for(int j=1;j<=i;j++){
        dp[i+1][j]=max(dp[i+1][j],dp[i][j]+arr[i+1][j]);
        dp[i+1][j+1]=max(dp[i+1][j+1],dp[i][j]+arr[i+1][j+1]);
    }
}

也可以这样写：

    for(int i=1;i<=r;i++){
        for(int j=1;j<=i;j++){
            dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+arr[i][j];
        }
    }

两种方法并没有太大的区别。

实际上不难发现，递归写法和递推的第二种写法是从问题的角度出发，而递归的第一种写法是从子问题推导出问题的解的角度出发的。

图论

DP与图论关系很大，图论中的Floyd算法和Dijkstra算法都采用的DP的思想。

实际上，如果将状态看作图上的点，将状态之间的关系看作边，那么DP实际上就是再一张图上用BFS跑最短路/最长路。BFS第一次访问的节点（第一层）就是DP的第一阶段。以次类推。

由于DP的特性无后效性，所以图中显然没有环，因此这个算法是正确的。  这也引出了有后效性的一个常见做法：利用SPFA算法的迭代思想，多次迭代到某个状态的最优解。