线段树小结

本文主要是对线段树在序列上的应用的简单讲解，并不涉及复杂的线段树应用。

从分治说起

众所周知，分治是一种常见的算法。序列上的分治通常是这种形式： 

1
2
3
4
5
result solve(int l, int r) {
    int mid = (l + r) >> 1;
    auto resl = solve(l, mid), resr = solve(mid + 1, r);
    return merge(resl, resr)
}
接下来考虑多次查询的情况。有的时候，我们不能接受调用多次 solve 的复杂度，因此要考虑优化。

首先，最简单的想法就是记忆化，然而问题在于，只需要稍微改变一下一开始询问的 l,r，最后调用的结果就会截然不同，永不上缓存的结果。因此，我们需要想方法增加重叠的子问题。

假如 merge 的实现分割点位置无关的话，将区间如何分成两段其实并不重要。我们可以先调用一次 solve(1,n)，把递归调用的 solve 的答案记录下来，然后使用保存下来的答案将对应的区间拼出来。如下图所示。 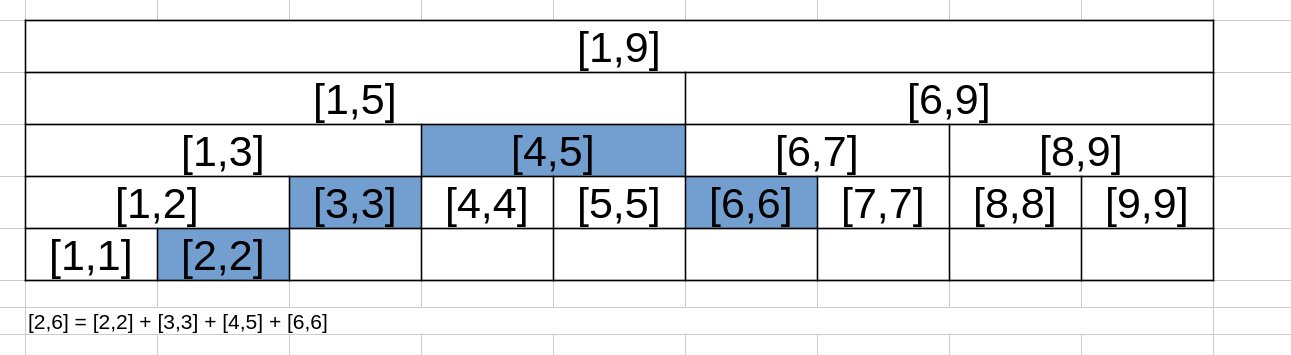简易线段树示意图 如上图蓝色区域所示，区间 \([2,6]\) 可以拆成 \([2,2],[3,3],[4,5],[6,6]\) 几个区间的结果合并起来。通常来说这样最多可以将区间分成 \(O(\log n)\) 个区间。注意到被保存下来的每个区间恰好对应两个区间，将每个保存下来的区间作为一个结点，向两个子区间连边，就形成了一颗二叉树。这颗二叉树就是线段树。

TIP 实现
对于二叉树的存储，我们可以开一个数组 a，每个结点 a[i] 对应的左右孩子分别对应 a[i*2] 和 a[i*2+1]。虽然线段树的结点个数最多只有 \(2n\) 个，但是这种编号方式最大编号可以达到 \(4n\)，需要开 \(4\) 倍空间。

这里是一个参考的区间 \(\max\) 实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
struct node {
    ll l, r;
    tag t; //稍后解释
    ll maxn;
    bool leaf() { return l == r; }
};

ll lc(ll x) { return 2 * x; }
ll rc(ll x) { return 2 * x + 1; }

ll query(ll p, ll l, ll r) {
    if (tree[p].leaf()) {
        return tree[p].maxn;
    }
    ll mid = (tree[p].l + tree[p].r) >> 1;
    ll res = -0x3f3f3f3f3f3f3f3f;
    spread(p); //稍后解释
    if (l <= mid) {
        res = max(query(lc(p), l, r), res);
    }
    if (mid + 1 <= r) {
        res = max(query(rc(p), l, r), res);
    }
    return res;
}

修改

显然线段树的功能不止于此。它还可以很方便地支持修改。

单点修改

注意到加入修改序列上的一个点 \(pos\)，受到影响的只有结点 \([pos,pos]\) 到根节点 \([1,n]\) 的 \(O(\log n)\) 个结点。对于每个结点的更新，在它的子节点更新完之后只需要在调用一次 merge 即可。因此实际上我们仅仅是调用了 \(O(\log n)\) 次 merge 而已。假设 merge 是 \(O(1)\) 的，单点修改的复杂度就是 \(O(\log n)\)。

区间修改

显然不可能对于区间中的每个点都修改。参考询问，将区间分成 \(O(\log n)\) 个子区间，对于每个子区间计算修改带来的代价。我们注意到并不是每个结点最后都会被用到，因此，对于这些子区间的子节点，我们可以考虑延迟更新结点，先在这些结点上打一个标记，仅当需要使用的时候再根据标记更新（“下传标记”）。这就是延迟标记。

TIP 实现
更新时，如果子节点原本就有标记，需要将标记合并，而不是简单的替换（尽管对于某些题目这两个操作是等价的）。对于标记十分复杂的情况，可以考虑定义一个结构体 tag，重载 operator+ 来计算一个 tag 对另一个 tag 的影响。同理，如果合并两个子节点的信息极为复杂，可以定义一个 update 函数来更新结点信息。另外，如果实现了区间修改，就没必要实现单点修改了。

参考实现（以区间加乘为例）： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
struct tag {
    ll times;
    ll add;
    tag() {
        times = 1;
        add = 0;
    }
    tag(ll _times, ll _add) : times(_times), add(_add) {}
    tag operator+=(const tag &b) {
        times *= b.times;
        add *= b.times;
        add += b.add;
        return *this;
    }
};

void update(ll p) { tree[p].maxn = max(tree[lc(p)].maxn, tree[rc(p)].maxn); }
void spread(ll p) {
    tree[lc(p)].t += tree[p].t;
    tree[lc(p)].maxn *= t.times;
    tree[lc(p)].maxn += t.add;
    tree[rc(p)].t += tree[p].t;
    tree[rc(p)].maxn *= t.times;
    tree[rc(p)].maxn += t.add;
    tree[p].t = tag();
}

void modify(ll p, ll l, ll r, tag op) {
    if (tree[p].leaf()) {
        tree[p].t += op;
        return;
    }
    ll mid = (tree[p].l + tree[p].r) >> 1;
    spread(p);
    if (l <= mid) {
        modify(lc(p), l, r, op);
    }
    if (mid + 1 <= r) {
        modify(rc(p), l, r, op);
    }
    update(p);
    return;
}

动态开点线段树

当维护的区间过于庞大时（例如，需要在 \(1\times 10 ^9\) 的值域上维护信息时），\(4\) 倍的空间变得难以承受。然而，并不是每个结点最后都会使用。因此，我们只在使用的时候才给这个点分配空间，这就是动态开点。此时需要在结点上记录左右子树的下标。通常采用数组加 new_node 函数来进行。 

1
2
3
4
5
6
7
node tree[N*60];// 此处大小需要自行计算。
ll cnt = 0;

//使用时：
tree[p].lc = cnt++;
tree[tree[p].lc] = node();
//...其他初始化操作

TIP 实现
应当避免使用 std::vector 来实现动态开点线段树。原因是 std::vector 的 push_back 会使迭代器失效，在递归过程中造成一系列问题。

参考题目

这些题目是用于加深理解的。限于篇幅，并不能一一讲解，可以参考对应题目的题解。

  • 洛谷 P1253 需要厘清如何合并标记。
  • 洛谷 P4198 虽然在讲解中我们都假设 merge 或者 update 是 \(O(1)\) 的，但实际上并非如此，只要最后的复杂度可以接受（具体题目具体分析）都可以使用。这题可以先考虑如何使用分治实现（如何合并两个区间的信息），在借助线段树的结构维护信息，优化复杂度。此外，一道题需要维护的信息不止一种，因此查询也可以有很多种。
  • 洛谷 P7453 这道题的前置知识是矩阵。更加复杂的更新与标记下传。

可持久化线段树

可持久化线段树可以支持在线的修改在历史版本上的修改，查询。最简单的方法就是每个修改新开一颗树，显然时空双飞。

正如我们之前提到的，单点修改最多影响 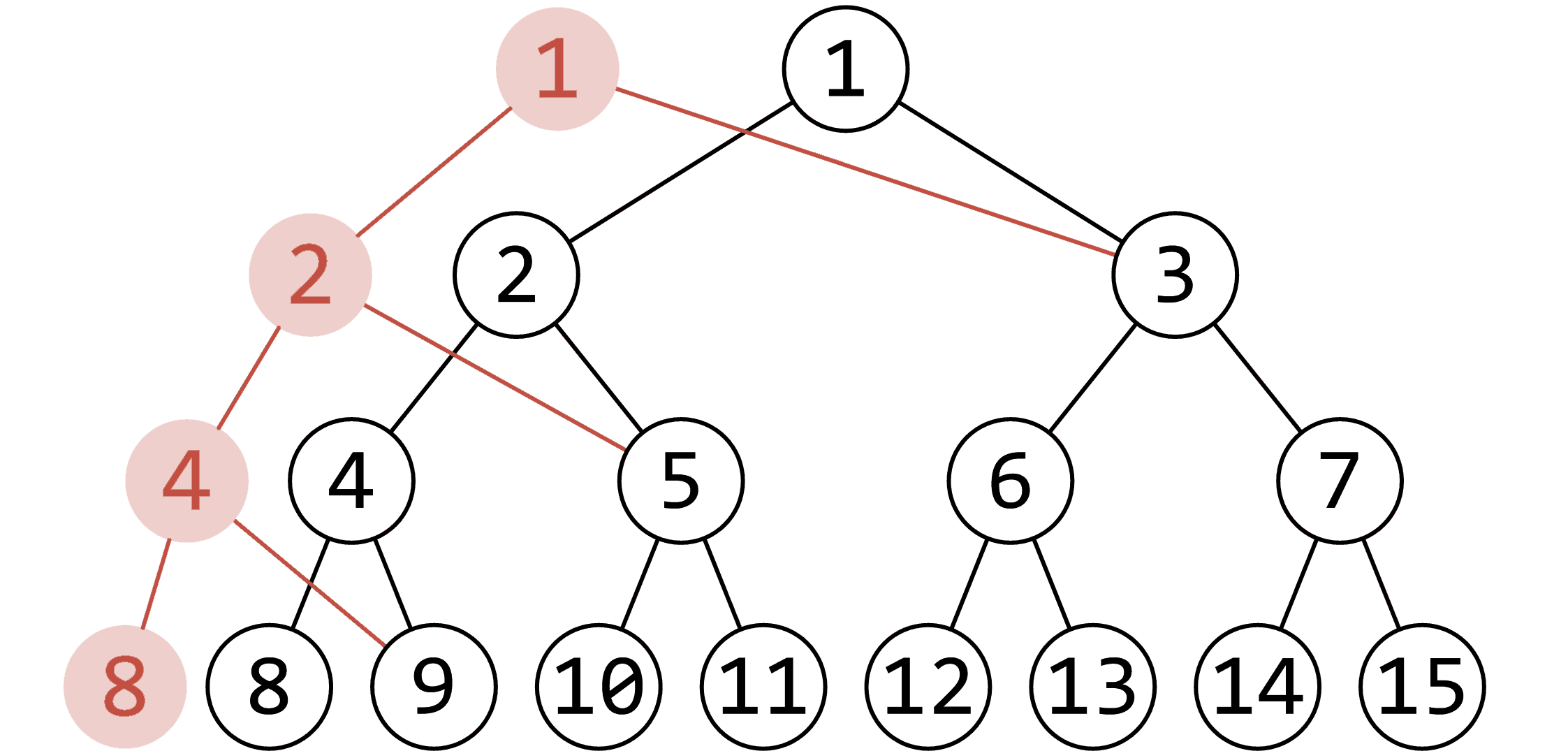\(O(\log n)\) 个结点。因此，我们只需要将这 \(O(\log n)\) 个结点复制一份，其余结点不变即可。具体的，假如当前修改到结点 \(p\)，结点 \(p\) 的左子树是受到影响的，则可以复制一份结点 \(p\)，其左子节点为复制一份后并修改的左子节点，有子节点为原先的右子节点。如果觉得有点抽象，可以看看 OI-Wiki 对应页面的这张图：可持久化线段树示意图 单次修改的时间复杂度仍是 \(O(\log n)\)，空间复杂度为 \(O(\log n)\)。

可持久化线段树的一个常见的用法是对于 \((l,r)\) 的询问将其转化成在 \(r\) 时刻的线段树查询一个和 \(l\) 有关的东西。结合例题来说一下。

洛谷 P1962 改。 给定一个长度为 \(n\) 的序列 \(A_i\)，\(q\) 次询问，每次回答 \([l,r]\) 之间的数去重后的个数。强制在线。 \(n,q\leq 1\times 10^6\)。

考虑就是扫描一遍数组，记录每个数上次出现的位置。假设数字 \(x\) 上一次出现在 \(prev_x\) 的位置，也就是 \(A_{prev_x}=x\)，维护一个数组 \(cnt\)，将 \(cnt_{prev_x}\) 加上 \(1\)。扫描到 \(r\) 时，\(\sum_{i=l}^r cnt_i\) 就是答案。

接下来，将这个 \(cnt\) 数组移到线段树上维护，利用可持久化线段树支持历史版本的查询，这道题就做完了。扫描的复杂度为 \(O(n\log n)\)，询问 \(O(q\log n)\)。

线段树二分

注意到线段树将区间分为左右两个的方式很适合二分。线段数二分就是在线段树上二分。具体的方法是首先检查左子节点的信息是否符合要求，如果是则递归到左子节点，否则递归到右子节点。

例如，我们要查询一颗权值线段树上第 \(k\) 大的数，就可以这样：

  • 查询左子节点数的总数 \(sum_l\)。
  • \(sum_l\geq k\)，查询左子节点第 \(k\) 大的数。
  • \(sum_l\lt k\)，查询右子节点第 \(k-sum_l\) 大的数。

线段树二分通常与可持久化线段树一起来对区间进行询问。比方说下面这个例题：求区间 \(\operatorname{mex}\)（洛谷 P4137）。

考虑一个数没有在一个区间 \([l,r]\) 出现意味着什么。意味着这个数 \(x\) 上一次出现的位置 \(prev_x\lt l\)。考虑像上一题一样从左到右扫描，维护每个数上次出现的位置 \(prev_x\)。这次，我们利用线段树维护 \(prev_x\) 数组，并且维护区间最小值。查询的时候，在 \(rt_r\) 上进行如下操作：

  • 查询左子节点的最小值 \(min_l\)。
  • \(min_l\lt l\)，说明左子节点至少有一个数没有在区间内出现，向左递归。
  • 否则，说明左子节点的左右数都出现了，向右侧递归。

单次复杂度 \(O(\log n)\)。

线段树分治

标记永久化

如果修改之间支持交换律，那么可以不下传标记，在询问时统计经过的标记对结果的影响。这个技巧在部分题目中相当有用。

例如：AtCoder AT_abc342_g。需要实现区间取 \(\max\)，删除操作以及查询。对于区间取 \(\max\)，我们在对应的节点上维护一个 mutiset（注意标记可能一样），查询的时候对于路径上的节点上的 mutiset 中的最大值取 \(\max\) 即可。删除时只需要找到对应的节点将标记 erase 即可。

线段树分治

接下来讲解线段树分治。考虑标记永久化，如果你需要在最后一次性询问每个下标该怎么办？要知道，并不是每道题目都可以只考虑节点上标记的其中一种一个造成的影响，有时你必须考虑所有标记（稍后你会看到）。考虑你查询完下标为 \(1\) 时的答案，接下来要询问下标为 \(2\) 的答案该怎么办？你只需要退回叶子节点 \([1,1],[2,2]\) 的 \(\operatorname{lca}\) 并撤销沿途标记造成的影响，然后走到节点 \([2,2]\) 并考虑沿途标记即可。接下来用类似的方法到 \([3,3],[4,4]\)。我们注意到这恰好构成了一次 DFS 的过程，你只需要在进入节点时考虑节点标记带来的影响，离开时撤销即可。

这就是线段树分治，一种离线算法，可以解决此类问题：动态插入，删除元素，询问一个问题（所有询问都相同）。线段树分治可以将插入和删除操作转化为插入和撤销操作。通常来说撤销操作都是较好实现的，只需要记录操作前的数据，撤销时还原即可。

线段树分治不仅可以运用在序列上，也可以运用在其他维度，比如时间。这也是线段树分治较为常见的用途。通过将插入和删除转化为时间上存在的区间，在线段树对应的节点上打上标记，最后一次 DFS 求出每个时间上的结果。

以洛谷 P5787为例，需要维护一个扩展域并查集来维护二分图。对于每条边，记录其存在时间 \([l,r]\)，意味着在第 \(l\) 次操作时加入，第 \(r+1\) 次操作时删除。在线段树上对应的结点上打个标记。接下来遍历线段树，进入某个结点时，将这个结点有标记的所有边加入并查集，到叶子节点时判断是否存在一个点的两个域在同一个集合里，在离开时撤销。

WARNING 实现
对于需要撤销的并查集，不能使用路径压缩，复杂度是假的。

线段树合并与分裂

权值线段树（通常是动态开点）支持合并与分裂。先说合并。

线段树合并

线段树合并的过程是这样的。

  • 同步遍历两颗线段树。
    • 如果只有一颗线段树上有这个节点，那么就直接将这个节点接在合并后的线段树上。
    • 如果两个都有，就递归合并左右节点。
    • 更新节点信息。

下面是参考代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ll merge(ll p1, ll p2) {
    if (p1 == -1) {
        return p2;
    }
    if (p2 == -1) {
        return p1;
    }
    if (tree[p1].l == tree[p1].r) {
        tree[p1].cnt += tree[p2].cnt;
        return p1;
    }
    tree[p1].lc = merge(tree[p1].lc, tree[p2].lc);
    tree[p1].rc = merge(tree[p1].rc, tree[p2].rc);
    update(p1);
    return p1;
}

假设两个线段树的点集为 \(A,B\)，合并这两颗线段树的复杂度为 \(O(|A\cup B|)\)。以下是简要证明。

  • 首先考虑共有的节点。显然需要 \(O(|A\cup B|)\)。
  • 接下来考虑这些节点的子节点。显然最坏情况下一个共有节点有两个子节点都不是共有的，需要 \(O(1)\) 的时间合并（直接接上去就行了）。总共是 \(O(|A\cup B|)\)。
  • 如果一个节点的父节点并不是共有节点，显然它会在它的某个祖先节点合并时被合并。不需要额外计算复杂度。

因而总共的复杂度就是 \(O(|A\cup B|)\)。

线段树分裂

权值线段树也支持分裂。举个例子，加入要把权值线段树前 \(k\) 项分裂出去，就可以这样做，将分裂后左右两侧的线段树记为 \(A,B\)：

  • 首先，考虑第 \(k\) 项在左节点还是右结点。
    • 如果在左节点，那么就将右节点接到 \(B\) 的对应节点上，向左节点递归。
    • 如果在右节点，那么就将左节点接到 \(A\) 的对应节点上，向右结点递归。

参考代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void split(ll rt, ll new_rt, ll dp) {
    // 根节点 新的根节点 分割点
    tree[new_rt] = tree[rt];
    tree[new_rt].lc = -1;
    tree[new_rt].rc = -1;
    if (tree[rt].l == tree[rt].r) {
        tree[new_rt].cnt = tree[rt].cnt - dp;
        tree[rt].cnt = dp;
        return;
    }
    if (tree[rt].lc != -1 && dp <= tree[tree[rt].lc].cnt) {
        tree[new_rt].lc = new_node();
        tree[new_rt].rc = tree[rt].rc;
        tree[rt].rc = -1;
        split(tree[rt].lc, tree[new_rt].lc, dp);
    }
    else {
        tree[new_rt].rc = new_node();
        split(tree[rt].rc, tree[new_rt].rc,
              dp - (tree[rt].lc == -1 ? 0 : tree[tree[rt].lc].cnt));
    }
    update(rt);
    update(new_rt);
    return;
}
单次复杂度为 \(O(\log n)\)。显然受影响的只有沿途的 \(\log n\) 个节点。

OI
#数据结构
线段树小结
https://blogs.sving1024.top/posts/20874/
发布于
2025年5月17日
许可协议