瞎谈点积

\(\newcommand{\lm}{\begin{bmatrix}}\newcommand{\rm}{\end{bmatrix}}\newcommand{\dis}[1]{\left\|#1\right\|}\) 从标题可以看出这篇文章时关于点积的。本文讨论的是平面点积。本文记 \(\vec{a}\) 的长度为 \(\left\|\vec{a}\right\|\)。

参与点积运算的是两个向量。架设有两个向量 \(\vec{a}=\begin{bmatrix}x_0 \\ y_0\end{bmatrix},\vec{b}=\begin{bmatrix}x_1 \\ y_1\end{bmatrix}\)，则我们定义点积为 \(\vec{a} \cdot \vec{b}=x_0x_1+y_0y_1\)。点积是一个很神奇的东西，先说它的几条性质。

性质

交换律

对于任意 \(\vec{a}=\begin{bmatrix}x_0 \\ y_0\end{bmatrix},\vec{b}=\begin{bmatrix}x_1 \\ y_1\end{bmatrix}\)，都有 \(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)。 证明：显而易见吧。 \[ \displaylines{ \vec{a} \cdot \vec{b}=x_0x_1+y_0y_1\\ \vec{b} \cdot \vec{a}=x_1x_0+y_1y_0=x_0x_1+y_0y_1 } \]

双线性

双线性意味着一下两点：

1. \(\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot \vec{b}+\vec{a}\cdot \vec{c}\)
2. \(\vec{a}\cdot(k\vec{b})=k(\vec{a}\cdot\vec{b})\) 证明都不难，根据定义展开计算即可，在这里不做赘述。

正定性

其实就是非负性

正定性意味着对于任何向量 \(\vec{a}\in \mathbb{R}^2\)，\(\vec{a}\cdot\vec{a}\geq 0\)。取等号当且仅当 \(\vec{a}\) 是零向量。

证明也很简单，假设 \(\vec{a}=\lm x\\y\rm\) 注意到 \(\vec{a}\cdot\vec{a}=x^2+y^2=\dis{\vec{a}}^2\)。显而易见，长度是不能为负的。

以上就是点积的三条性质，这些性质大多用来参与运算。

关系

这还不是点积最神奇的地方，最神奇的地方在于点积和两个向量的长度和夹角都有关。

1. 对于单位圆上的向量 \(\vec{a},\vec{b}\)，其夹角为 \(\theta\)，都有 \(\vec{a}\cdot\vec{b}=\cos \theta\)。

   证明：假设向量 \(\vec{b}\) 是由 \(\vec{a}\) 逆时针 \(\theta\) 度之后得到的，由于众所周知，逆时针旋转 \(\theta\) 度之后 的旋转矩阵是 \(\lm \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \rm\)。设 \(\vec{a}=\lm x\\y\rm\)，那么有 \(\vec{b}=\vec{a}\lm \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \rm=\lm x\\y\rm \lm \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \rm=\lm x\cos\theta-y\sin\theta \\ x\sin\theta+y\cos\theta\rm\)。所以 \[\displaylines{\vec{a}\cdot\vec{b}& =x(x\cos\theta-y\sin\theta)+y(x\sin\theta+y\cos\theta)\\& =x^2\cos\theta-xy\sin \theta+xy\sin \theta +y^2\cos\theta\\& =(x^2+y^2)\cos \theta=\dis{\vec{a}}\cos \theta=\cos \theta}\] 证毕。

2. \(\vec{a}\cdot\vec{b}=\dis{\vec{a}}\dis{\vec{b}}\cos\theta\)。

   证明：既然有了单位向量点积的关系，我们不如将这两个向量转化为单位向量。显然 \(\dfrac{1}{\dis{\vec{a}}}\vec{a},\dfrac{1}{\dis{\vec{b}}}\vec{b}\) 都是单位向量，而且夹角的大小不变。因此 \((\dfrac{1}{\dis{\vec{a}}}\vec{a})\cdot(\dfrac{1}{\dis{\vec{b}}}\vec{b})=\cos\theta\)。再用双线性得\(\dfrac{1}{\dis{\vec{a}}\dis{\vec{b}}}(\vec{a}\cdot\vec{b})=\cos\theta\)，移项就可以得到 \(\vec{a}\cdot\vec{b}=\dis{\vec{a}}\dis{\vec{b}}\cos\theta\)。这也说明了一点，就是两个向量垂直当且仅当点积等于一，因为这时候 \(\cos\theta=0\)。

以上两点可以看出，点积和参与运算向量的长度和夹角都有关。为什么呢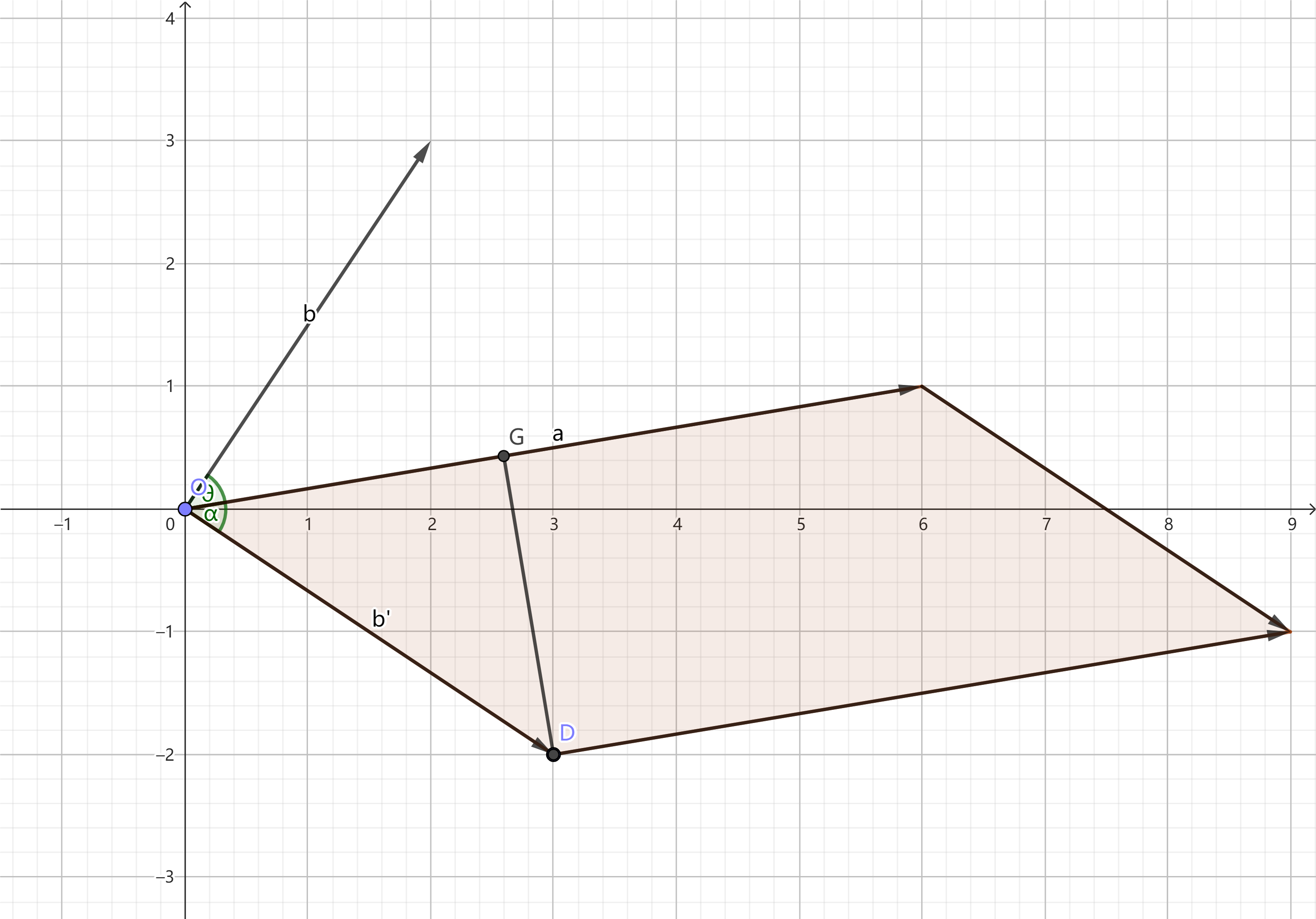？ 如图，设\(\vec{a}=\lm x_0\\y_0\rm,\vec{b}=\lm x_1 \\ y_1 \rm\)将 \(\vec{b}\) 顺时针旋转 \(90^\circ\) 后得到 \(b^\prime =\lm y_1\\-x_1\rm\)，因此整个阴影四边形的面积就是 \(\operatorname{det}(\lm y_1 & x_0\\-x_1& y_0 \rm)=y_0y_1-(-x_1x_0)=x_0x_1+y_0y_1\)，恰好是 \(\vec{a}\cdot\vec{b}\) 如果你不懂行列式，也没关系。根据三角函数我们可以知道 \[GD=\dis{\vec{b^\prime}}\sin\alpha=\dis{\vec{b}}\sin\alpha=\dis{\vec{b}}\cos(90^\circ -\alpha)=\dis{\vec{b}}\cos\theta\] 所以平行四边形的面积为 \(\dis{\vec{a}}\dis{\vec{b}}\cos\theta\)。这样就解释了为什么点积和长度，夹角都有关系。行列式不也是吗

应用

由于这些神奇的特性，我们可以有点积做一些有趣的事情。

正交分解公式

也可以叫投影公式，起这个标题只是因为听起来更高大上。

这个公式的作用是这样的：给定两个向量 \(\vec{a},\vec{b}\)，将 \(\vec{a}\) 拆成 \(\vec{a_0}+\vec{a_1}\) 的形式，使得 \(\vec{a_0}\perp \vec{b},\vec{a_1}\parallel \vec{b}\)。其中一个方法是线性变换，另一个就是点积。

先给出一个解析几何的方法： 假设 \(\vec{a}=\vec{a_0}+\vec{a_1}\)，由于 \(\vec{a_1}\parallel\vec{b}\)，所以我们可以设 \(\vec{a_1}=k\vec{b}\)，可以得到 \(\vec{a}=\vec{a_0}+k\vec{b}\)，两边同时点积得 \(\vec{a}\cdot\vec{b}=\vec{a_0}\cdot\vec{b}+k(\vec{b}\cdot\vec{b})\)，由于 \(\vec{a_0}\perp \vec{b}\)，所以 \(\vec{a_0}\cdot\vec{b}=0\)。因此 \(\vec{a}\cdot\vec{b}=k(\vec{b}\cdot\vec{b})\)，\(k=\dfrac{\vec{a}\cdot\vec{b}}{\vec{b}\cdot\vec{b}}\)。带入得 \(\vec{a_1}=\dfrac{\vec{a}\cdot\vec{b}}{\vec{b}\cdot\vec{b}}\vec{b}\)。这是怎么发现的

再给出一个其他的理解方法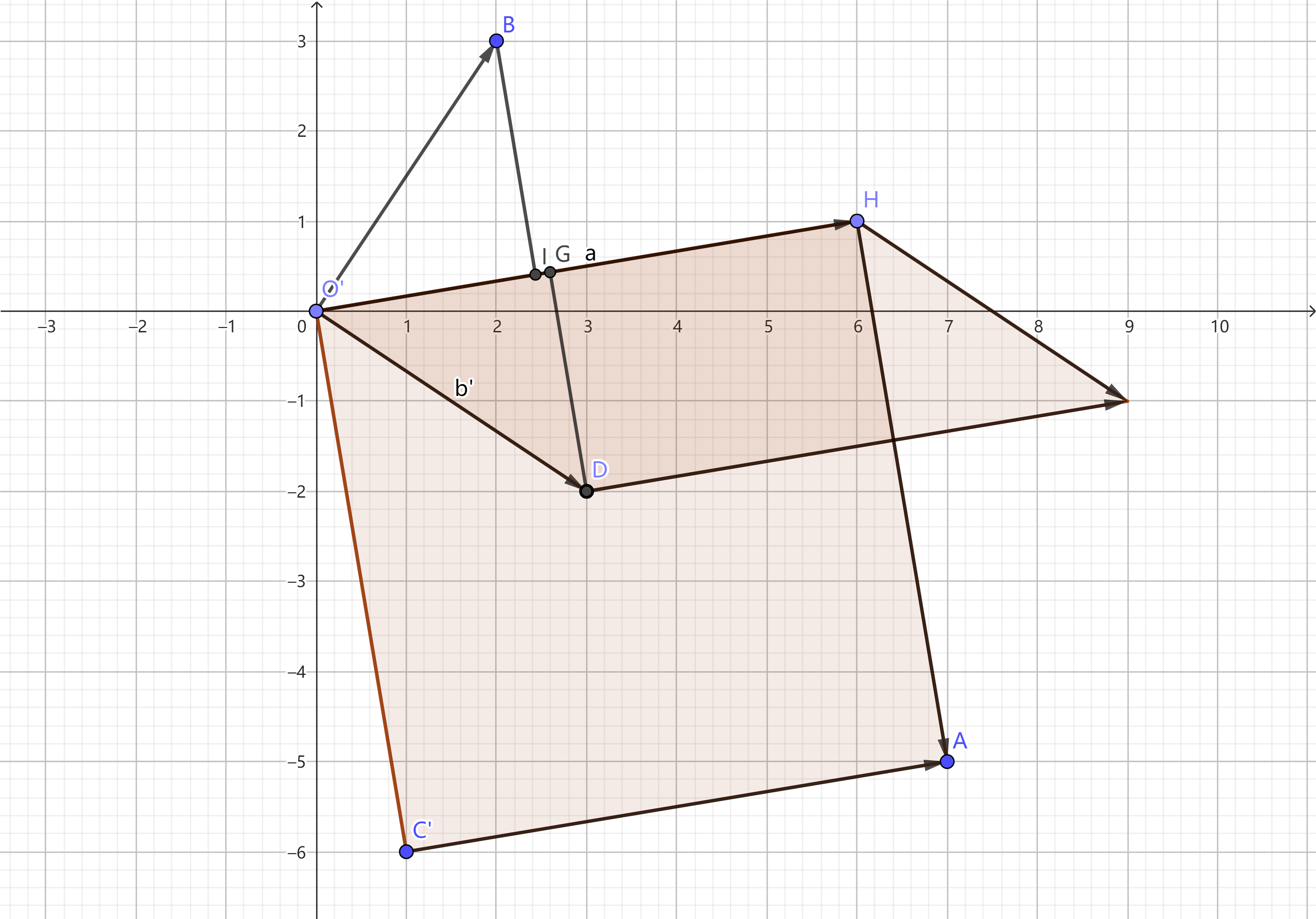： 容易看出，\(\dfrac{\vec{a}\cdot\vec{b}}{\vec{b}\cdot\vec{b}}\) 实际上是 \(GD\) 和 \(OC\) 的比值，等于 \(OI\) 和 \(OH\) 的比值（通过三垂直可以知道 \(\triangle BGO \cong \triangle OGD\)）。因此将这个数乘上 \(\vec{b}\) 自然就是 \(\vec{OI}\)，也就是得到的 \(\vec{a_1}\)，太好了，数学诚不我欺。

柯西不等式

柯西不等式，又叫Cauchy-Schwarz不等式，指的是这个 \(\left|\vec{a}\cdot\vec{b}\right|\leq \dis{\vec{a}}\dis{\vec{b}}\)。结合刚才的平行四边形和 \(\vec{a}\cdot\vec{b}=\dis{\vec{a}}\dis{\vec{b}}\cos\theta\) 可以很快推出来，因为 \(\cos\theta\) 在 \([-1,+1]\) 之间，取 \(\pm 1\) 时当前仅当 \(\theta=0^\circ\)。

还有另外一种证明方法，就是将 \(\vec{a}\) 进行正交分解，得 \(\vec{a}=\vec{a_0}+\vec{a_1}\)。移项得 \(\vec{a_0}=\vec{a}-\vec{a_1}\)，两边同时点积得 \[ \displaylines{ \vec{a_0}\cdot\vec{a_0}&=\vec{a_0}\cdot(\vec{a}-\vec{a_1})\\ &= \vec{a_0}\cdot\vec{a}-\vec{a_0}\cdot\vec{a_0}\\ &= \vec{a_0}\cdot\vec{a}\\ &= (\vec{a}-\dfrac{\vec{a}\cdot\vec{b}}{\vec{b}\cdot\vec{b}}\vec{b})\cdot\vec{a}\\ &= \vec{a}\cdot\vec{a}-\dfrac{\vec{a}\cdot\vec{b}}{\vec{b}\cdot\vec{b}}(\vec{a}\cdot\vec{b})\\ &= \dis{\vec{a}}^2-\dfrac{(\vec{a}\cdot\vec{b})^2}{\dis{\vec{b_0}}^2}=\dis{\vec{a_0}}\geq 0 } \] 整理得 \[ \displaylines{ \dis{\vec{a}}^2-\dfrac{(\vec{a}\cdot\vec{b})^2}{\dis{\vec{b_0}}^2}\geq 0\\ \dis{\vec{a}}^2\geq \dfrac{(\vec{a}\cdot\vec{b})^2}{\dis{\vec{b_0}}^2}\\ \dis{\vec{a}}^2\dis{\vec{b_0}}^2\ge(\vec{a}\cdot\vec{b})^2\\ \sqrt{\dis{\vec{a}}^2\dis{\vec{b_0}}^2}\ge\sqrt{(\vec{a}\cdot\vec{b})^2}\\ \dis{\vec{a}}\dis{\vec{b_0}}\geq \left|\vec{a}\cdot\vec{b}\right|\\ } \] 证毕。