凸透镜与凹透镜
凸透镜
成像原理
关于实像和虚像的定义，请参见实像和虚像
众所周知，凸透镜有聚光的作用。
- 在一倍焦距以内，一个点光源发出的光线最后是这样的：
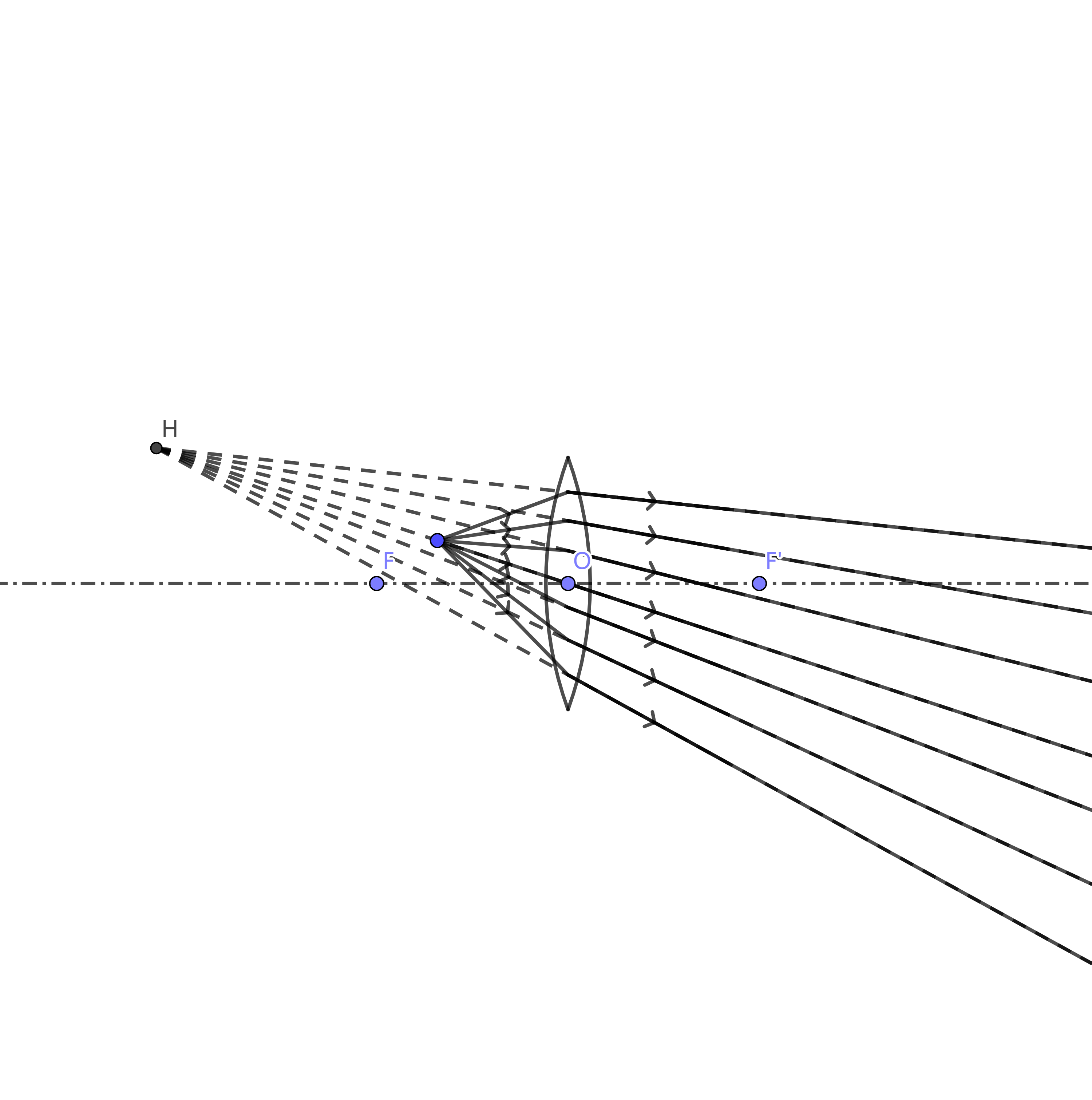此时经过凸透镜的光线的反射延长线交于H点，这个点光源会在H点成虚像。由于光线会比原来汇聚，所以H点到透镜的距离会大于点光源到透镜的距离。 - 当点光源位于一倍焦距之外是，光线是这个样子的。
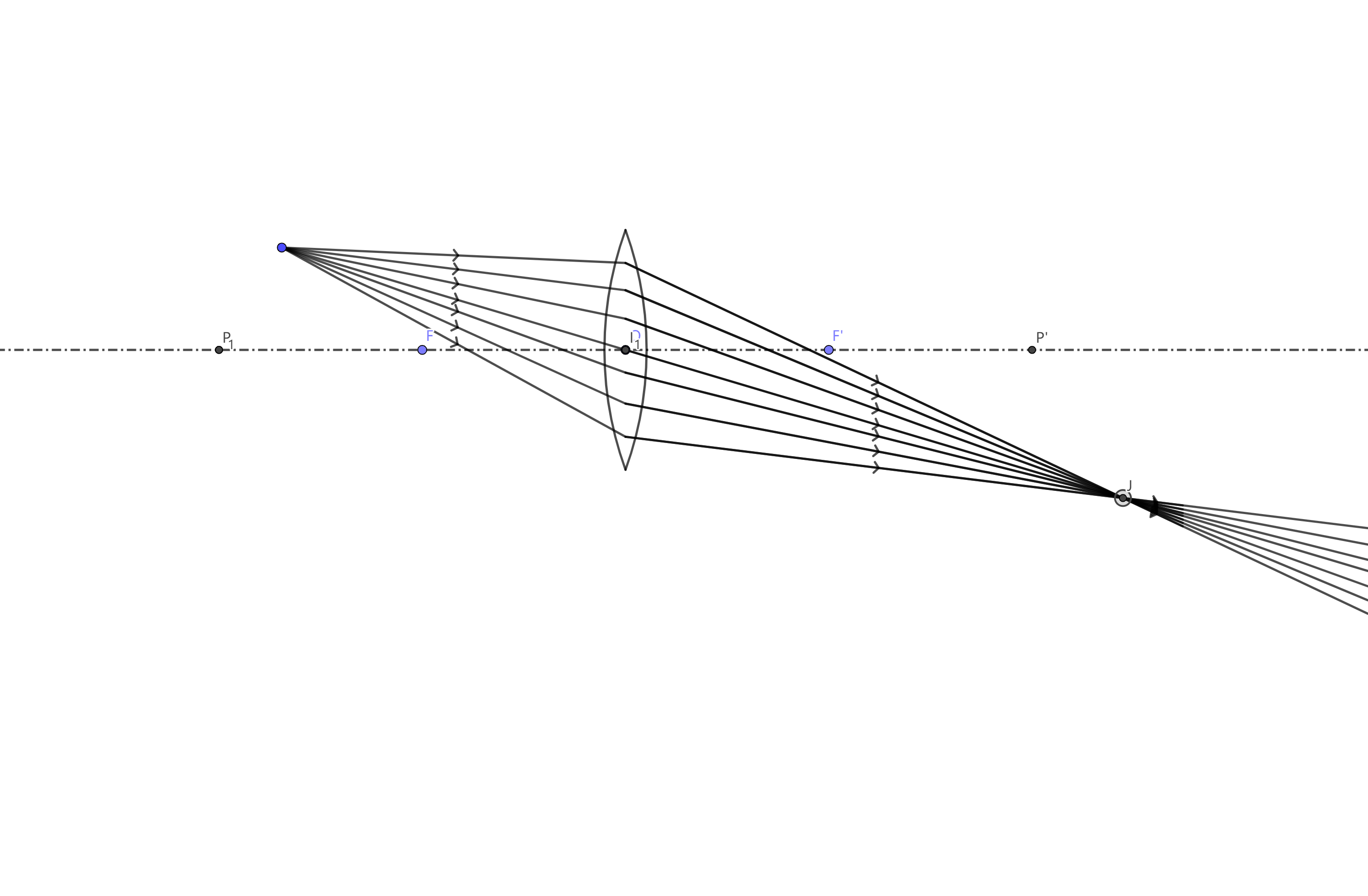此时经过凸透镜的光线会交于J点，再J点放置光屏，可以再光屏上成实像（即，J点会成点光源的实像）。这时，如果再J点右侧观察，J点相当于一个点光源（但是并不是点光源，只是有相同的效果）。
注：其实并不是只有一个点光源发出的光线会像这样汇聚成一点，满足这些条件的光线可以不是从同一个光源上发出的，但是这些光线一定是等价于一个点光源发出的光线（折射时光路可逆），因此，我们可以用这些点光源代替这些光线。
有了这些知识，我们就可以理解凸透镜的成像原理了。
- \(u\lt
f\)时（方便起见
就是懒，以后只保留关键光路）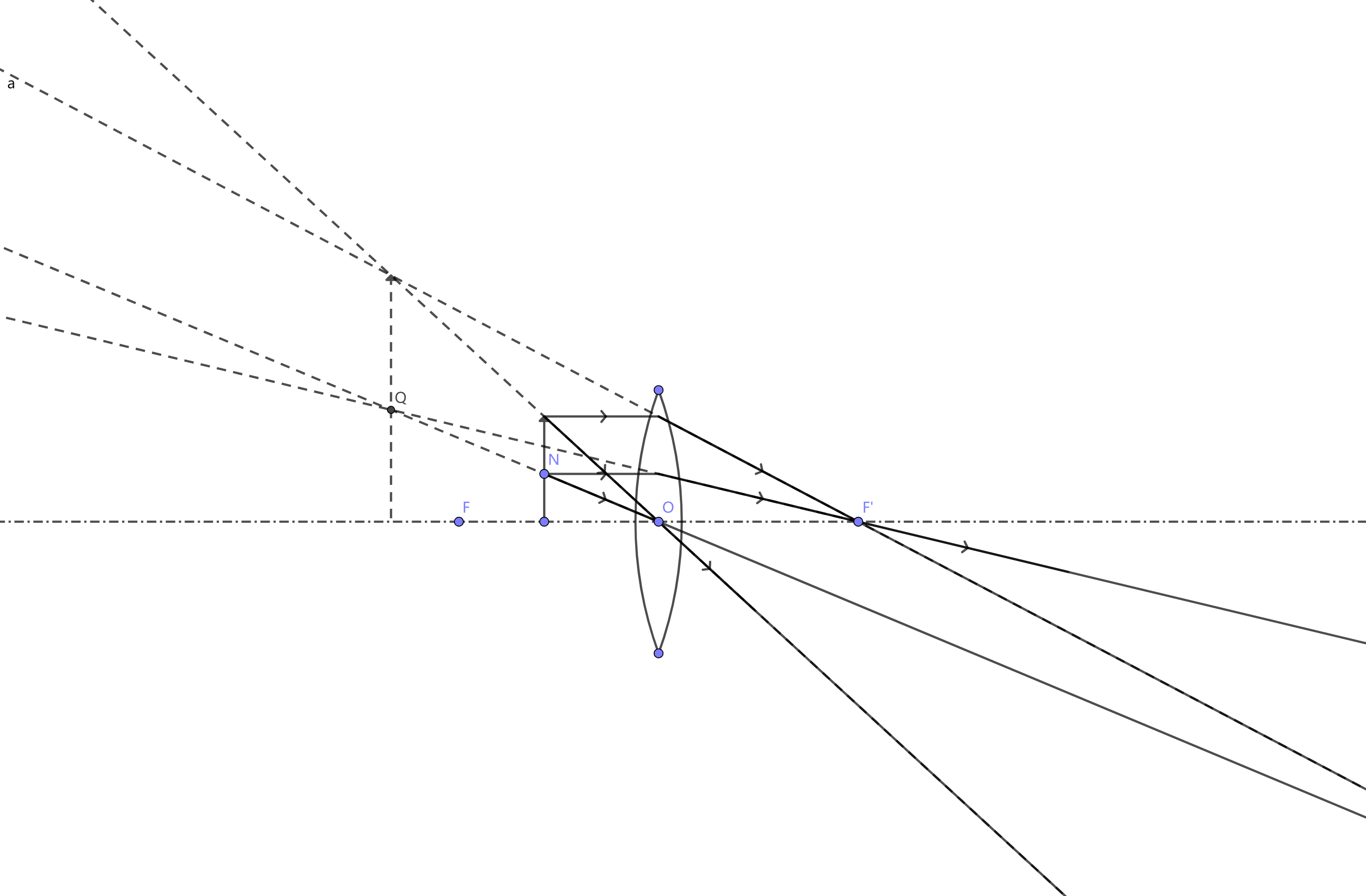
每个光源上的点光源会在同侧成虚像，点光源的所有虚像一起构成了光源的虚像。 - \(u\gt f\)时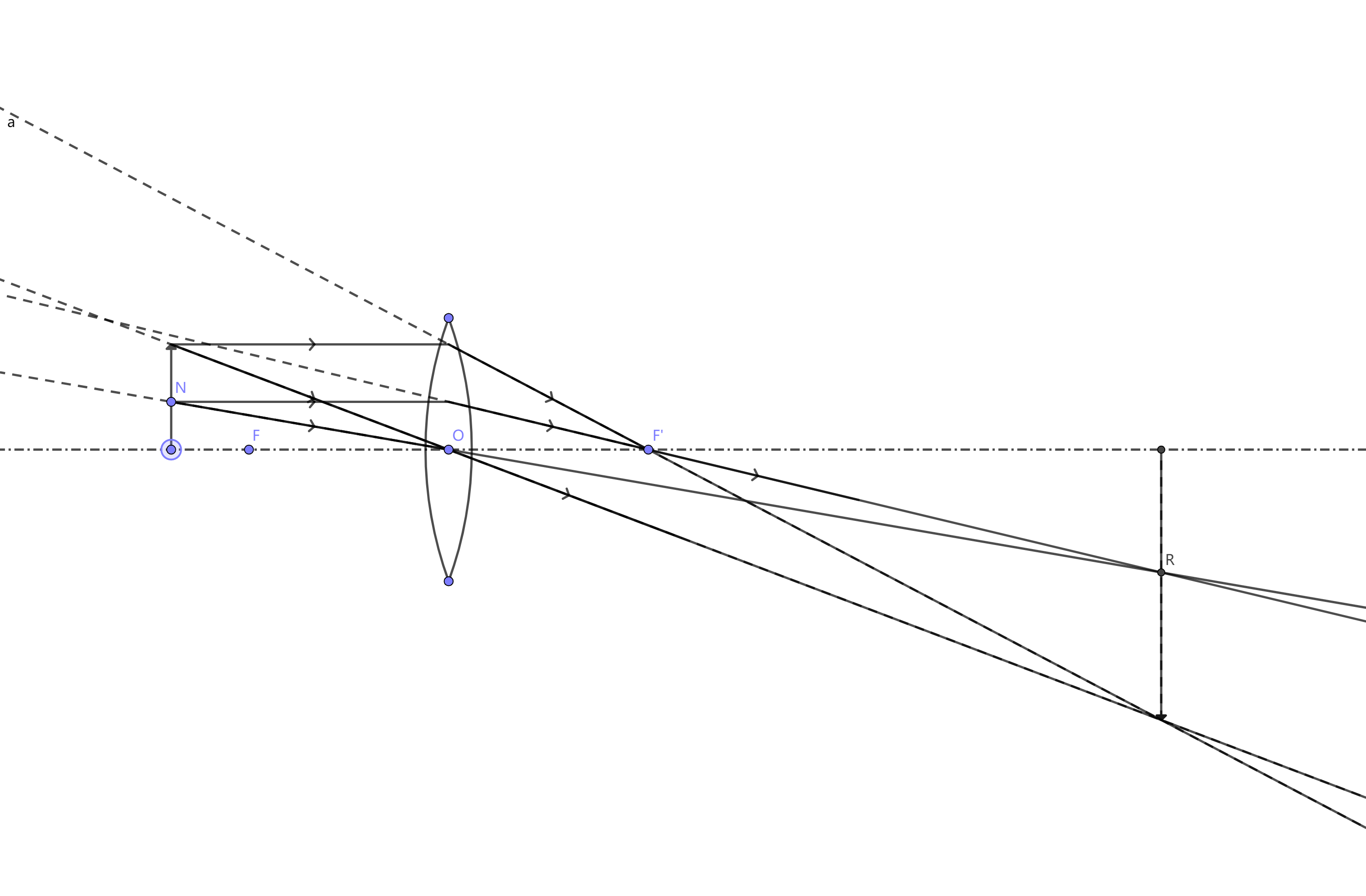
光源上的每个点光源发出的光线经过透镜后汇聚在另一侧的一个点上，这些点一起构成了实像（即，在另一侧成实像），在像的右侧，会有一个等效与光源的”光源“，有每个点光源的等效光源组成。
最后，关于眼睛看到的东西： - 成虚像时：看到的就是虚像。
- 成实像时：在实像右侧时，由于每个点光源会在右侧形成一个等效的“点光源”，眼球会调节焦距直到这些“点光源”在视网膜上成实像，这些“点光源”在视网膜上一起构成了光源的像，所以我们可以透过凸透镜看见像（像的位置就是实像所在的位置）。在实像左侧观测时，光路不等价与任何点光源发出的光路，所以大脑无法处理这些光路，什么像都观测不到。
为什么只能透过透镜看到部分像？
假设眼睛在T点，那么这些光线是眼睛可以看到的（光路保留临界光线）：
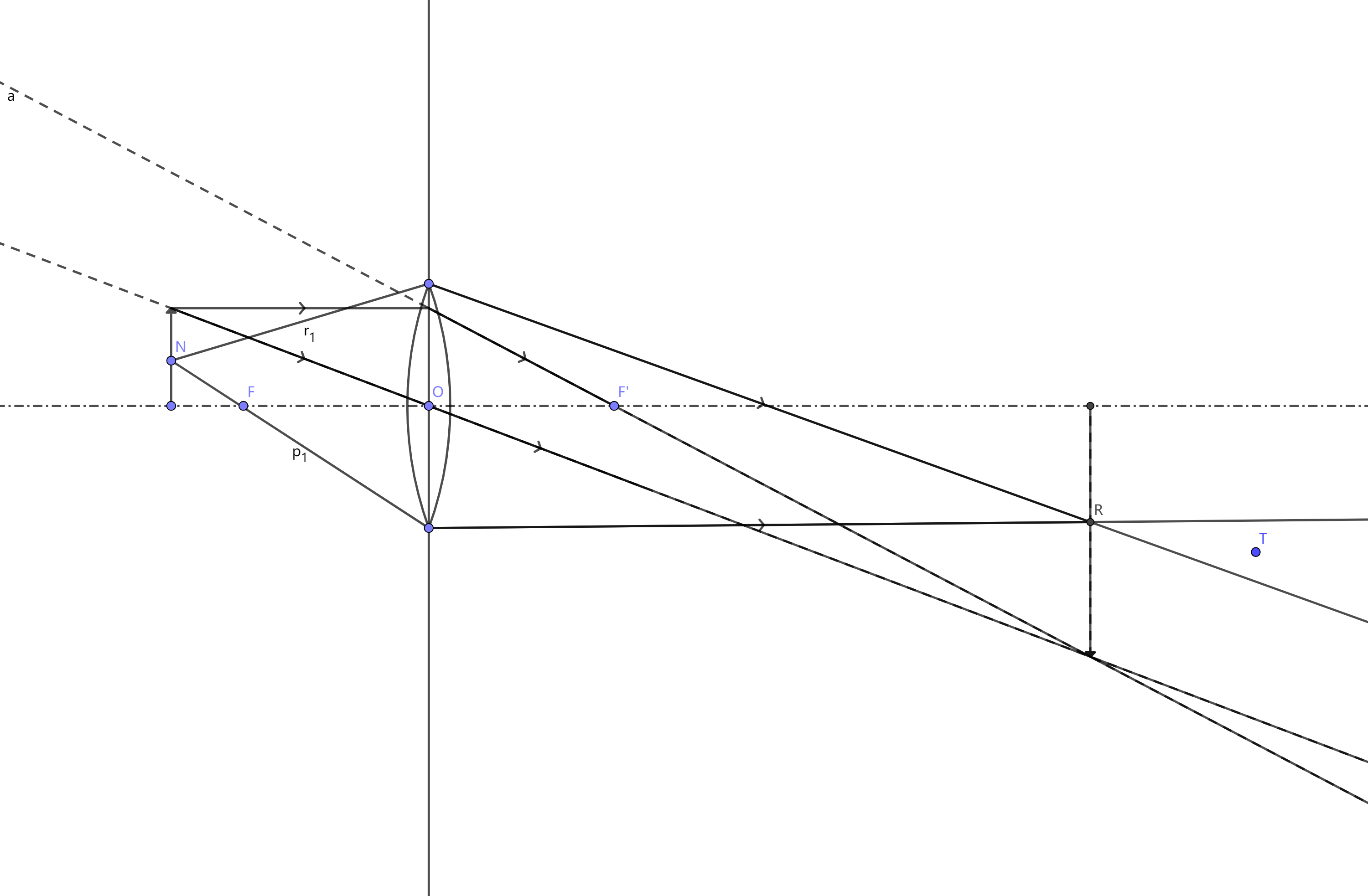这些是看不到的： 
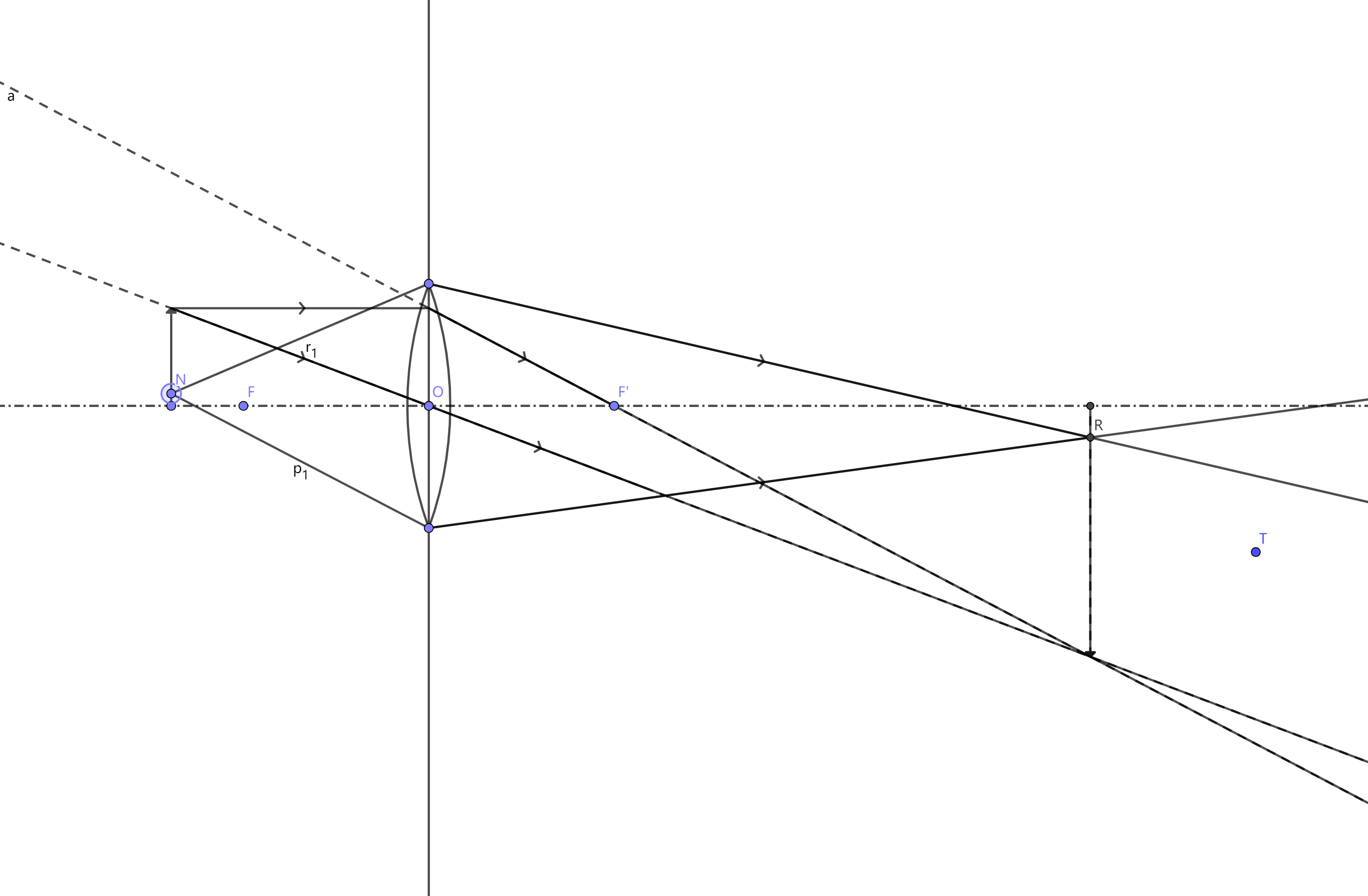所以只能看到一部分。
焦距、物距和相距
对于凸透镜来说，焦距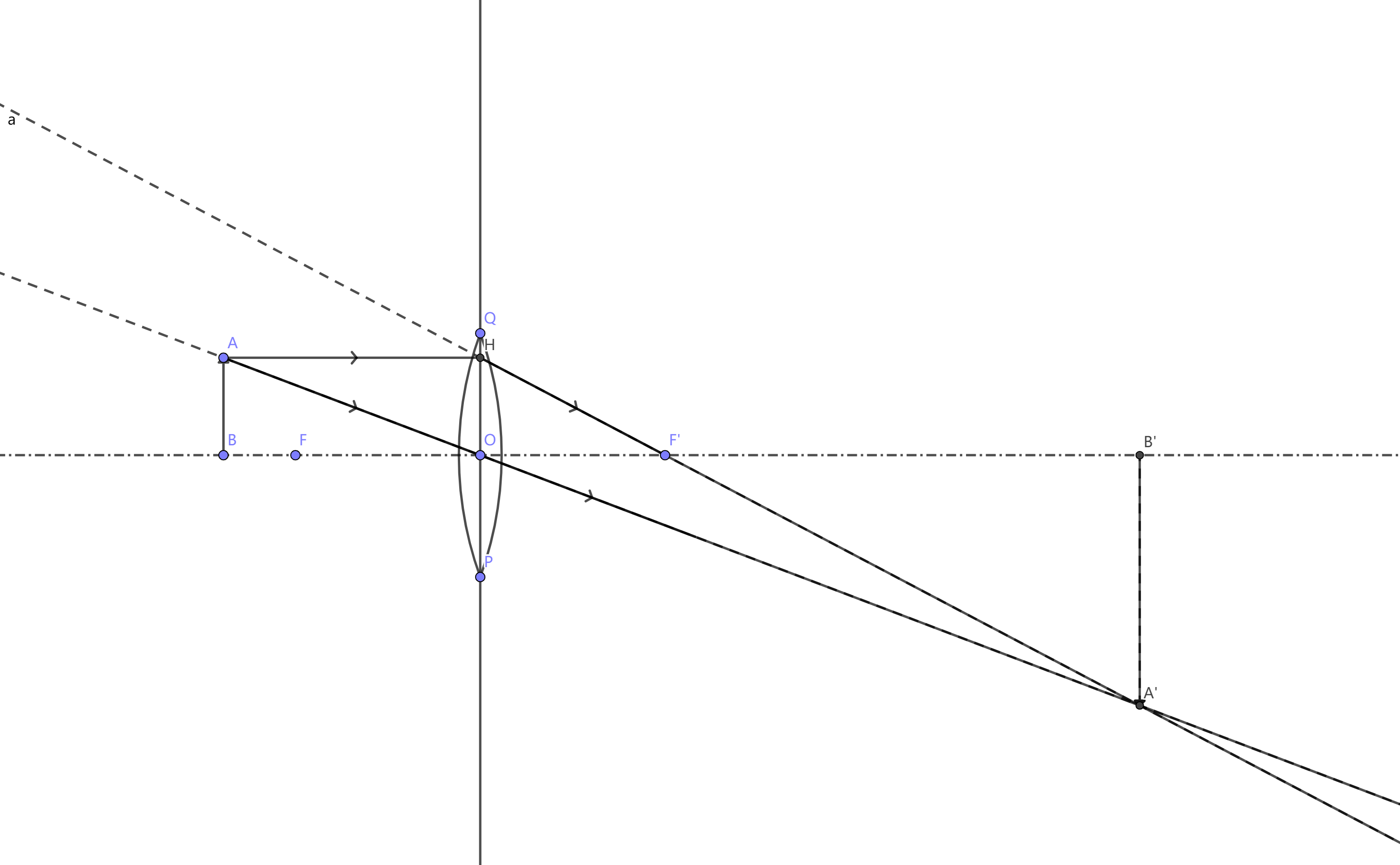\(f\)、物距\(u\)和相距\(v\)有这样的关系： \[
\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}
\] 证明：还是这张图 
\[
\displaylines{
物距u=BO,相距v=B'O,焦距f=OF=OF' \\
易证\triangle{ABO}\sim\triangle{A'B'O}且\triangle{HOF'}\sim\triangle{A'B'F'}
\\
\therefore AB:A'B=BO:B'O=u:v,\\
HO:A'B'=OF':B'F'=f:v-f\\
\because AB=HO\\
\therefore AB:A'B=HO:A'B\\
\therefore u:v=f:(v-f)\\
vf=u(v-f)\\
vf=uv-uf\\
vf+uf=uv\\
(u+v)f=uv\\
u+v=\dfrac{uv}{f}\\
\dfrac{u+v}{uv}=\dfrac{1}{f}\\
\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}
}
\]
眼球
晶状体本质上是一个凸透镜，外界光源通过这个透镜将像成在视网膜上，由感光细胞接受，由大脑处理形成了视觉。 和所有凸透镜成像一样，最后在视网膜上成一个点的像不一定来自于一个点光源，最后的像也不一定是由实际的物发出的，眼睛只关心最后入眼的光线汇聚再视网膜上能不能成清晰的像。但是，如果可以，那么此时入眼的光线仍等价与一个光源的光线（既然等价，自然成的像一样，所以我们一般用这个光源来代替入眼光线）。
显微镜和望远镜
原理
这两个原理是一样的，都是凸透镜组合，我们把靠近物的叫做物镜，另一个叫做目镜。物镜成实像，将在透镜右侧形成一个等效的”光源“（实像），目镜成”光源“的放大的虚像（起放大的作用）。 为什么一定要用透镜组？ 1. 单个透镜成实像：作为望远镜时，并不能起到望远的作用，因为像时缩小的（参见凸透镜成像规律）。作为显微镜，显然放大倍数不够大（或足够大的难以生产），而且不方便观测（人不一定在像的外侧，要人左右移动）。 2. 单个透镜成虚像：对于两者：放大倍数都不够大（况且虚像会比原来远）。 为什么一定要采用这种形式？ 如果物镜成虚像，由于凸透镜成虚像到透镜的距离会较物距更远，不便控制第二个目镜在放大倍数够大时一定成虚像。 如果目镜成实像，那么观测时不一定在像的右侧，看到实像，需要人来回移动（而且有时实像很远），也不方便。
大于两个透镜组合
只要保证最后一个凸透镜成虚像，剩下的成实像，保证凸透镜之间的距离即可。
透镜间距离
记相邻2个透镜距离\(d\).透镜1焦距\(f_1\)，透镜2焦距\(f_2\)，物距相距同理。 清晰范围：指将\(d\)调节到该范围可以得到清晰的像（这个范围需要保证透镜1成的像在透镜2的成像范围之内）。 可调节范围：指对于每一个物距\(u_1\)，都能在这个范围内调节\(d\)得到清晰的像。（就是在设计显微镜和望远镜时，设定的\(d\)可以调整的范围）。
望远镜
清晰：\(v_1\lt d\lt v_1+f_2\)（范围内改变会导致虚像大小改变） 可调节范围（假设\(u_1\gt 2f_1\)）\(f_1\lt d\lt 2f_1+f_2\)
显微镜
清晰：\(v_1\lt d\lt v_1+f_2\)（范围内改变会导致虚像大小改变） 可调节范围（假设\(f_1\lt u_1\lt 2f_1\)）\(d\gt 2f_1\)
多个透镜组合
清晰：对于任意两个相邻的透镜（不包括倒数第一个和倒数第二个，即，两个透镜都成实像）都有\(v_1+f_2\lt d\)（范围内改变会导致第二个镜头成的实像和\(v_2\)改变,第二个透镜成放大像是有\(v_1+f_2\lt d\lt v_1+2f_2\),成缩小像时有\(d\gt v_1+2f_2\)），对于最后两个透镜，满足\(v_1\lt d\lt v_1+f_2\)。 可调节范围：对于两个成实像的透镜，\(f_1+f_2\lt d\)，对于最后两个透镜，\(d\gt 2f_1\).
凹透镜
与凸透镜成虚像时差不多，只是相距小于物距，大小缩小，并且只成虚像。
视力矫正
近视眼看不起远处的物体，就让凹透镜将像成近一些（\(v\lt u\)），就可以看清楚了。 远视眼看不起近处的物体，就让凸透镜将像成远一些（\(u\gt v\)），就可以看清楚了。