容斥
折线法
定义变换 为关于直线 镜射（轴对称）。
两条直线
感觉骗我呢题解里说的似乎不是很易于理解（不过这里也可能不怎么好理解就是了）。
考虑如下问题：如图，记录点 到点 的路径条数，要求不能碰到直线 或者 。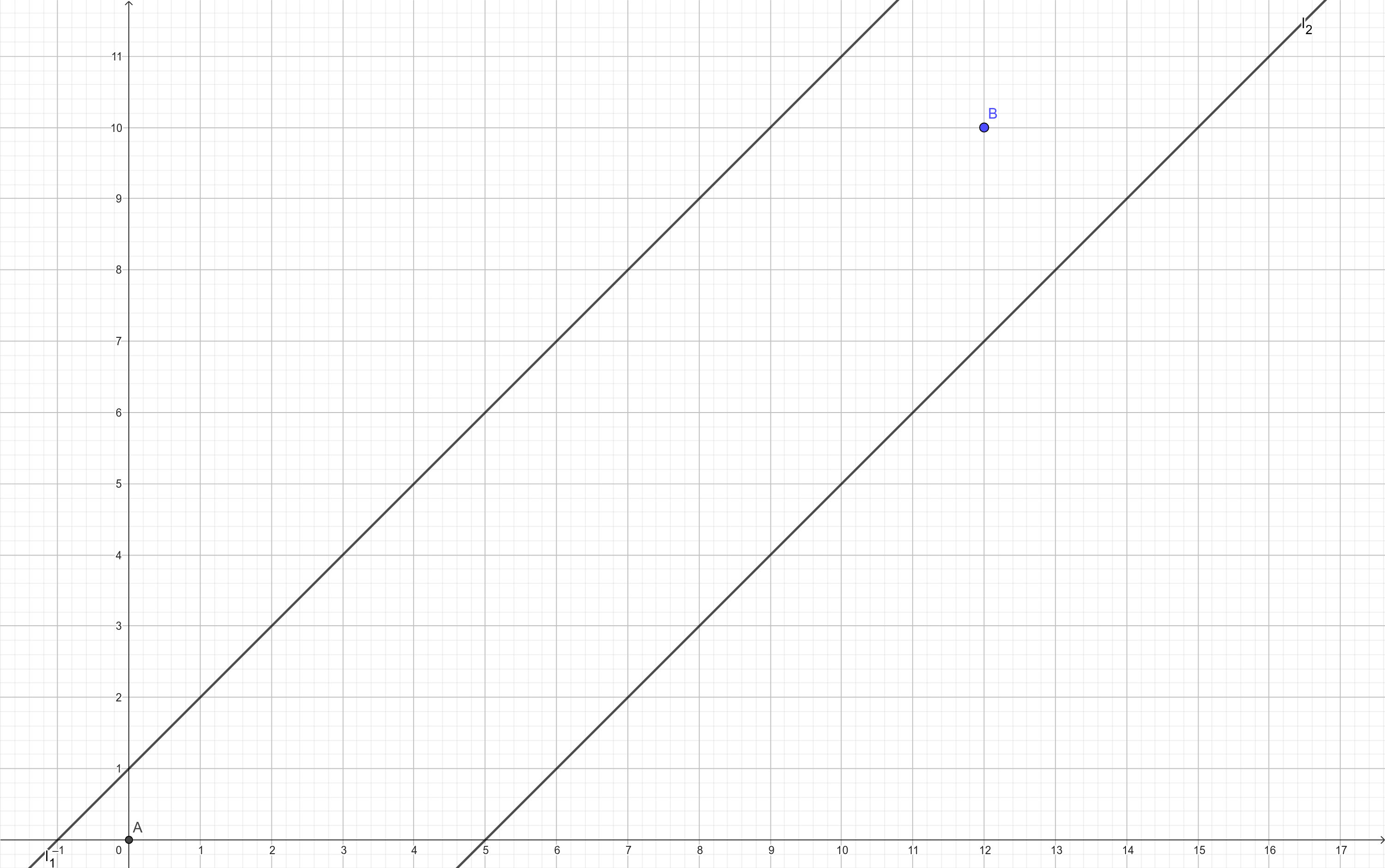 
先考虑对路径编号。我们一次写下路径与哪条直线相交（与 相交就写下 ，与 相交就写下 ），对于连续的一段 或 ，我们只保留其中一个。 考虑一条路径。如下图所示。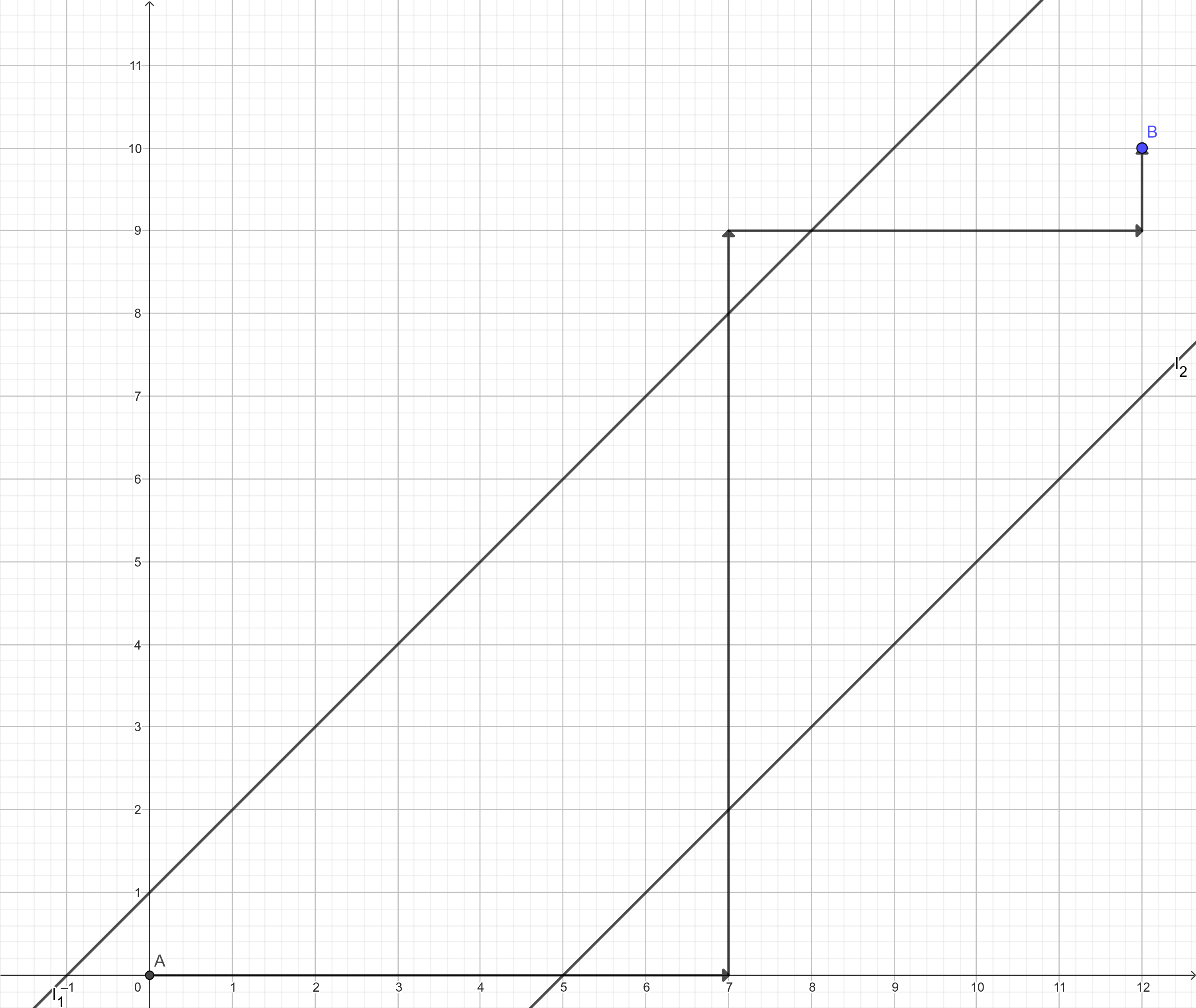 
这条直线先与 有 个交点，然后与 有 个交点。依次写下来，就是 ，连续的两个 和 只保留 个，最后我们将其记作 。
显然所有的路径都可以编号为一个 交替出现的序列，记这个序列为 。令 为以 为前缀的路径条数。显然，最后符合条件的路径个数就是 考虑计算。先来考虑 。仿照一条直线的情况，我们取和 的第一个交点，将这之后的路径关于 镜射。另 。计算 到 的路径条数，这个就是从 到 并且至少碰到一次 的条数。注意，我们只考虑了至少碰到 次，而没有保证第一次就碰到 。考虑路径在和 第一次相交之前的部分。
- 之前的部分和谁都没有相交。也就是说，第一次碰到的就是 。这类路径的个数就是 。
- 根据定义，这部分路径是在和 第一次相交之前。因此显然不可能和 相交。
- 之前的部分和 相交了。此类路径的条数是 。下图就是其中一条：
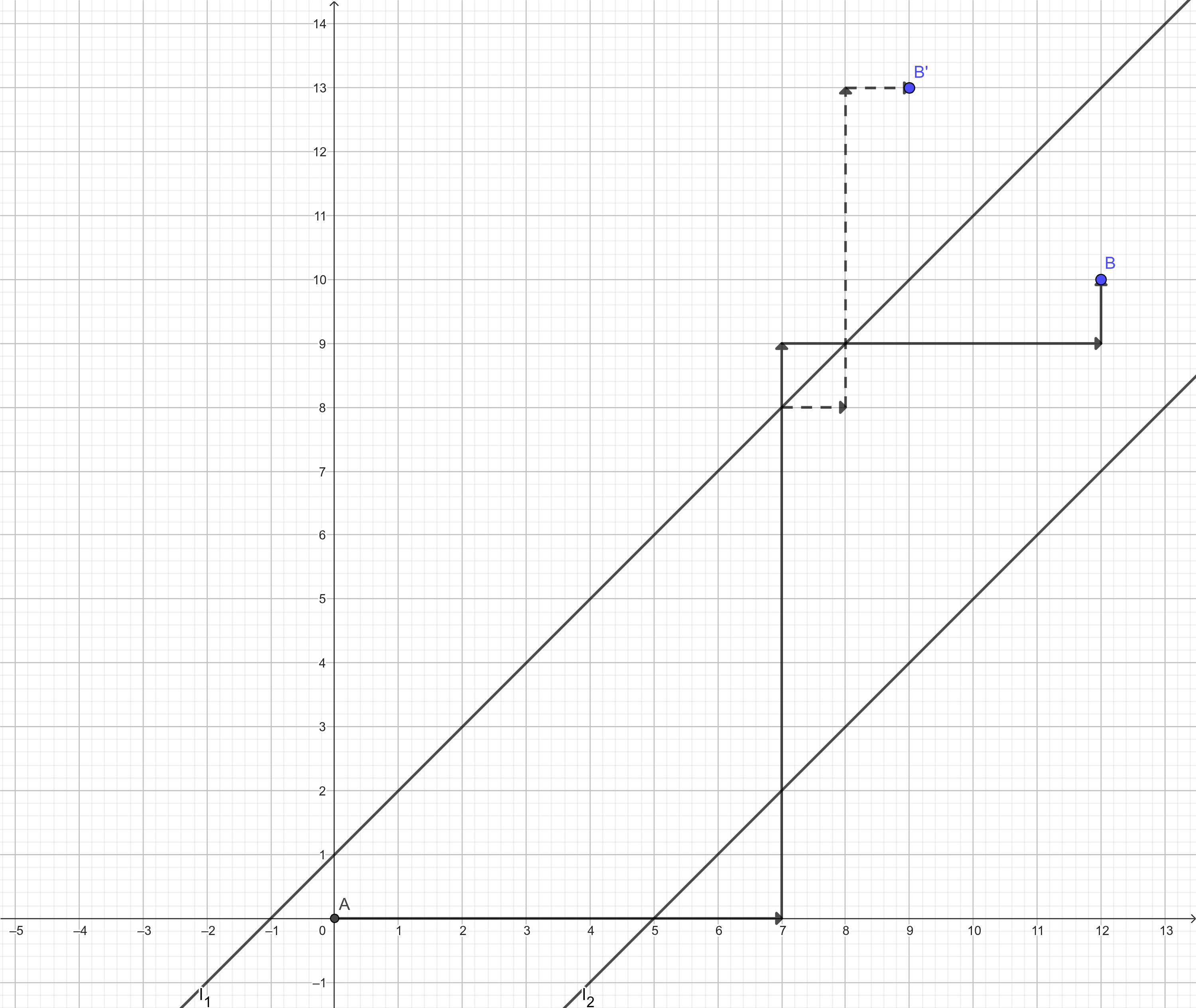
因此，这样算出来的路径条数实际上是 。因此我们需要减去 。
我们可以考虑找到路径中第一次 出现的位置（注意，不是第一次和 相交也不是第一次和 相交），先将重点关于 镜射，再关于 镜射得到 ，计算 到 的路径条数。和上面一样，由于我们不知道之前是否与两条直线相交过，因此这样算出来的路径条数实际上是 。
继续镜射，直到某个时刻镜射后的点 不再第一象限内，此时路径条数就是 。然后将其一路回带，就可以算出 的值。 也是类似的流程，不再赘述。对于 的情况，复杂度为 。
斯特林数
第一类斯特林数