城市游戏题解

模仿直方图中最大的矩形的求法，把地图分行处理，将下一行看作是累加再上一行后面的矩形，当出现R时我们认为矩形缺了一块。

先考虑题目的一种简单情况：两边矩形的边界都在扩大，如图所示

那么要求出其中最大矩形的面积，我们可以考虑将每个矩形的高度作为结果矩形的高，宽度延展到右边界得到的面积。再这个例子中，就是这几个矩形中的最大值
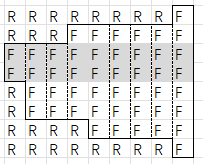此时考虑左侧有分叉的情况，比如：
此时，再考虑有分叉的行的时候，只要考虑矩形分成各个小段后，各个小段的高度作为矩形的高度，宽度延展到右边界的矩形中最大的一个最大值即可。例如再考虑第4列时，应该考虑这两个矩形面积的最大值。
注意到宽度一定，所以高度高的面积就大。注意到这两种情况都有一个共同点，就是后面的矩形都可以覆盖前面的矩形。因此，我们可以维护一个具有这样性质的单调栈。

接下来考虑插入的情况。

1. 如果新插入的矩形不会改变单调性，直接插入。
2. 如果新插入的矩形会改变单调性，那么持续弹出栈顶，依次考虑每个矩形，更新最大值。注意到再这样考虑完之后，只有可以与新插入的矩型会参与后面的计算，其余部分则是无用的，因此我们用这个矩形来替代原矩形。比如这张图中红色部分则是无用的。
   注意，由于每个矩形的形状不同，因此最后保留的部分也不一定相同，再弹出时要比较与上一个矩形是否完全一样，如果是再累加长度，否则新开一个矩形。比如下图中黄色和蓝色两个矩形都是被保留下来的，但是形状不一样。
   

我们可以用一个二进制整数来存储矩形的长度（1代表F，0代表R），用按位或运算来检验是否可以完全覆盖，用按位与得到保留下来的矩形，扫描最长的连续1的长度得到高度。考虑到答案范围较大，因此可以使用std::bitset来存储。

这个算法的复杂度是：单调栈 ，扫描得到最大连续一的长度 ，由于每次更新都要扫描，因此总复杂度是 。

参考代码：（由于代码中大量使用stl，常数较大，因此手动开启O2优化。复杂度是正确的）

#include <iostream>
#include <bitset>
#include <stack>
using namespace std;

struct node{
    bitset<1005> b;
    int width;
    int maxl;
};

int n,m;

int max_lenth(const bitset<1005>& b){
    int ans=0;
    int res=0;
    for(int i=0;i<m;i++){
        if(b[i+1]==1){
            res++;
        }
        else{
            ans=max(ans,res);
            res=0;
        }
    }
    ans=max(ans,res);
    return ans;
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr),cout.tie(nullptr);
    cin>>n>>m;
    int ans=0;
    stack<node> s;
    for(int i=0;i<n;i++){
        bitset<1005> bi;
        stack<node> temp;
        for(int j=0;j<m;j++,bi<<=1){
            char x;
            cin>>x;
            if(x=='F'){
                bi^=1;
            }
        }
        temp.push({bi,1,max_lenth(bi)});
        int width=0;
        while(!s.empty()&&(bi|s.top().b)!=bi){
            width+=s.top().width;
            if((bi&s.top().b)==temp.top().b){
                auto x=temp.top();
                temp.pop();
                x.width+=s.top().width;
                temp.push(x);
            }
            else{
	            temp.push({(bi&s.top().b),s.top().width,max_lenth(bi&s.top().b)});
            }
            ans=max(ans,s.top().maxl*width);
            s.pop();
        }
        while(!temp.empty()){
            s.push(temp.top());
            temp.pop();
        }
    }
    int w=0;
    while(!s.empty()){
        w+=s.top().width;
        ans=max(ans,s.top().maxl*w);
        s.pop();
    }
    cout<<ans*3<<endl;
    return 0;
}